In a nutshell
A simple test that finds a positive relationship between deviations from Benford’s law and the applicable tax or tariff rate may be suggestive of evasion taking place.
Such a test could be applied to import flows using a particular mode of transport, crossing a particular checkpoint or even being cleared by a particular customs officer.
The test could be performed using import transaction data that are collected by customs and hence available almost immediately.
Wherever taxes are being collected, there is tax evasion, border taxes being no exception. Yet by its very nature, tax evasion is difficult to detect as the parties involved have every incentive to conceal their lack of compliance with the law. The recent surge in trade protectionism makes the need to detect non-compliance even more urgent, as higher tariffs give trading parties powerful incentives to engage in evasion.
In a recent study (Demir and Javorcik, 2020), we propose a new method for detecting tax evasion in international trade, based on deviations from Benford’s law. We apply it in the context of an unexpected increase in border taxes in Turkey and find evidence consistent with an immediate increase in tax evasion associated with the affected import flows.
Benford’s law
Benford’s law describes the distribution of first (leading) digits in economic or accounting data. Contrary to what one might expect, the leading digits in various types of numerical data are not uniformly distributed – that is, the occurrence of digits 1 to 9 as the first digit in a recorded number is not equally likely.
Instead, numbers are more likely to begin with a low digit, such as 1, 2 and 3 than with a high digit, such as 7, 8 or 9. According to the formula proposed by the law, on average numbers tend to start with the digit 1 30% of the time, while 9 is the leading digit only 4.6% of the time (see Figure 1).
Figure 1: Benford’s distribution of first digits
Notes: The figure shows the distribution of the leading first digits as predicted by Benford’s law: Prob (First digit is d) = log10(1 + 1/d).
The law naturally arises when data are generated by an exponential process or independent processes are pooled together. To date, deviations from Benford’s distribution have been used to detect reporting irregularities in macroeconomic data (Michalski and Stoltz, 2013) and in survey data (Judge and Schechter, 2009).
Data manipulated for the purpose of evasion are likely to display significant deviations from Benford’s law. This is because, as experimental research shows, people do a poor job of replicating known data-generating processes, by, for example, over-supplying modes or under-supplying long runs (Camerer, 2003).
Moreover, since Benford’s law is not widely known, it seems very unlikely that those manipulating numbers would seek to preserve fit with the Benford distribution.
Why Benford’s law should hold in import data
One can expect Benford’s law to hold in international trade data for two reasons:
- First, ‘second-generation’ distributions – that is, combinations of other distributions, such as, quantity times price (as in trade transaction values) – conform with Benford’s law (Hill, 1995).
- Second, Benford’s law holds for right-skewed distributions – that is, distributions where the mean is greater than the median (Durtschi et al, 2004), which is a characteristic of import values.
Using detailed customs figures from Turkey, we show that exports, as well as imports that are not subject to tariffs (or other import duties), conform to Benford’s law. In contrast, imports that are subject to import duties show visible deviations from Benford’s law.
Applying Benford’s law to Turkish imports data
We consider an unexpected trade policy change in Turkey. On 13 October 2011, the Resource Utilization Support Fund tax, which applies to imports using external financing, increased from 3% to 6% of the transaction value. Because not all import varieties (defined as product-country combinations) were equally reliant on foreign financing and hence subject to the tax, we can examine whether there was a systematic relationship between a variety’s exposure to the tax in the initial period and observed deviation from Benford’s law after the tax increase.
We use detailed imports data, disaggregated by the exporting firm, product, source country, month-year and financing terms for the period from October 2009 to September 2012. Exposure to the tax is measured as the share of imports coming with external financing at the variety level in the 12 months before the policy change.
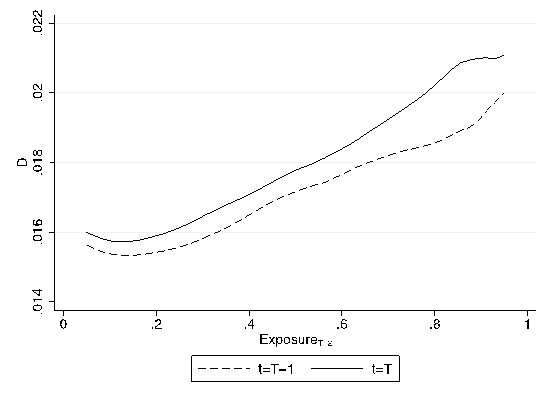
As illustrated in Figure 2, we find that deviations from Benford’s law are positively associated with exposure to the tax already 12 months before the policy change (see the dashed line). This relationship becomes even stronger in the 12 months after the tax increase (see the solid line).
Strikingly, the gap between the two lines is wider at the higher levels of exposure, which is consistent with an increase in tax evasion after the tax doubled. This conclusion is further confirmed by a formal econometric exercise.
To gain confidence in our result, we also apply an alternative and well-established method proposed by Fisman and Wei (2004). The method relies on comparing data on exports to Turkey as recorded by foreign trading partners with Turkey’s own import statistics. We find that the gap between the recorded exports and imports increases more for varieties with greater exposure to the tax increase in the initial period, thus confirming our conclusions based on Benford’s law.
Figure 2: Deviations from Benford’s law and exposure
Notes: The figure shows local polynomial regressions of Turkish imports reported by the source country and Turkey as functions of Exposure, which is defined as the share of imports with external financing at time t = T – 2 (24-months before the policy change at t=T). Source: Demir and Javorcik (2020)
Conclusion
Our study has practical implications. A simple test showing a positive relationship between deviations from Benford’s law and the applicable tax or tariff rate may be suggestive of evasion taking place and thus calls for further scrutiny
Such a test could be applied to import flows using a particular mode of transport, crossing a particular checkpoint or even being cleared by a particular customs officer. The test could be performed using import transaction data that are collected by customs and hence available almost immediately.
Based on such an analysis, the authorities could to decide where to channel resources in their fight against evasion.
Further reading
Camerer, C (2003) Behavioral Game Theory: Experiments in Strategic Interaction, New Age International.
Demir, B, and B Javorcik (2020) ‘Trade Policy Changes, Tax Evasion and Benford’s Law’, Journal of Development Economics, forthcoming.
Durtschi, C, W Hillison and C Pacini (2004) ‘Effective Use of Benford’s Law to Assist in Detecting Fraud in Accounting Data’, Journal of Forensic Accounting 4.
Fisman, R, and S-J Wei (2004) ‘Tax Rates and Tax Evasion: Evidence from ‘Missing Imports in China’, Journal of Political Economy 112(2): 471-500.
Hill, TP (1995) ‘A Statistical Derivation of the Significant-Digit Law Detecting Problems in Survey Data Using Benford’s Law’, Statistical Science 4.
Judge, G, and L Schechter (2009) ‘Detecting Problems in Survey Data Using Benford’s Law’, Journal of Human Resources 44(1).
Michalski, T, and G Stoltz (2013) ‘Do Countries Falsify Economic Data Strategically? Some Evidence That They Might’, Review of Economics and Statistics 95(2): 591-616.